Глава 8. Анализ вывода формулы спектральных серий атома

                водорода на основе постулатов Бора. Квантовые числа.                                                                                                                   

        С тех  пор, как  я  впервые ознакомился с постулатами Бора и выводом на их основе формулы спектральных  серий, меня не  покидала  мысль, что  совпадение  результатов расчетов по этой формуле с опытными данными не случайно. Эта мысль  имела веские основания. Я не мог себе представить, как несколько величин, связанных между собой определенными отношениями, могли случайно выразить реальную закономерность. С другой стороны возникали сомнения. Вывод формулы основывался на планетарной модели строения атома Резерфорда, которая не представляла внутреннюю  структуру электрона, а потому он считался цельным (монолитным) телом. Такое представление не давало  объяснения постулатам  Бора, хотя  явно  и  не  противоречило им (то, что электрон при своем вращении вокруг ядра должен был бы быстро потерять  энергию, ни  на  чем не основывалось - было надумано). Появившаяся позднее квантовая теория также не внесла определенности в строение атома. Напротив, появился, так называемый, принцип  неопределенности, согласно  которому   положение электрона в атоме определялось вероятностью нахождения его в некотором объеме. Структура электрона опять же не  рассматривалась, и  оставалось  не  ясным, что  он  из себя представляет. Впрочем, считалось, что это уже и не имеет никакого  значения, ибо  квантовая  теория, представляющая  собой череду абстрактных нагромождений, в ряде  случаев  противоречащих  друг другу, позволяла  объяснять  все по библейскому принципу: "Так было богу угодно".

     Сомнения вызывал и сам расчет энергии электрона в атоме водорода, производимый Бором. Энергия  получалась  отрицательной, а  это  уже не укладывается ни в какие представления. Еще можно  смириться  с  отрицательным  значением  относительной энергии. Однако в расчетах Бора мы имеем отрицательное значение абсолютной энергии электрона. Можно было предположить, что причина здесь кроется в наделении электрона энергией, ему не принадлежащей - потенциальной. Это общее заблуждение, когда энергия, так называемого поля (гравитационного, электрического, магнитного) приписывается телу, находящемуся в этом поле. А потому, казалось бы, энергия тела может быть принята отрицательной по отношению к энергии поля. Но и это неверно, так как энергия поля действительно определяет потенциальную энергию тела находящегося в нем, – под влиянием энергии поля (объективно: под влиянием потока эфира) тело может приобрести кинетическую энергию.

       Чтобы не быть голословным в несогласии с мнением о существовании отрицательной энергии, можно привести следующие рассуждения.

        Полная энергия волновой частицы

 

                                            E = m V ²

 

        Из этой формулы видно, что носителем энергии  является  материя, то  есть ее масса. Масса не может принимать отрицательных значений - она либо есть, либо ее нет. Скорость V может принимать любые значения - и положительные и отрицательные. Но даже если она отрицательна E = m (-V)² = m V ², то есть энергия все равно положительна.

       И, тем не менее, я длительное время не мог получить формулу спектральных серий атома водорода при положительном значении его энергии. Я далеко не сразу понял, что попал под стереотип чужого мышления.

       Для того чтобы  привести вывод спектральных серий атома водорода в соответствие с новой концепцией необходимо было осмыслить уравнения, использовавшиеся Бором. Первое уравнение выражало динамическое  равновесие  вращающегося  вокруг  протона электрона:

 

 1                                 m V ²/r = ke²/r ²,

 

где по современным представлениям  m –  масса электрона,  V – его орбитальная скорость, r –  радиус орбиты, k = 9×10⁹  , e –  заряд электрона.

     Равенство 1 можно преобразовать и представить в виде:

 

                                          mV ² = ke²/r

 

     Уравнение 1 решалось Бором совместно с постулатом, выраженным равенством:

 

  2                                 mVr = nh/2p,

 

где  h -постоянная Планка, n -целое число.

     Современная теория  объясняет  правомерность  постулата Бора универсальным равенством, определяющим постоянную  Планка:

 

  3                                      mV l = h ,

 

где   m -масса любого тела, V-его скорость,  l-длина волны, которая является абстрактной величиной, так как не понятно из  чего  состоит  сама волна. Для постулата Бора было принято, что   l = 2pr/n , где  r - радиус орбиты электрона, n - количество волн де Бройля. Однако физическую сущность этих волн определить невозможно, и уж тем более я не нахожу их связи с  волнами, значение  длины которых входит в универсальное равенство 3.

       В соответствие с новой концепцией постоянная Планка выражает постоянство   импульса   энергии   одной   вторичной волны сферона (или общей волны фотона)

4                                     h  =   mV l

 Длина вторичной волны может быть принята равной длине поперечных волн, то есть

                                           l = 2pr/n

Подставив в равенство 4 получим:

 

                                       mV r = nh / 2p,*

 

то есть мы пришли к равенству, выражающему постулат Бора.

     Энергия вторичных волн в главной волне электрона

5                                                          W = nm_вV ² = mV ²,

где n – количество вторичных волн, m_в – масса одной вторичной волны, V – скорость распространения этих волн в теле главной волны электрона.

       Энергия W складывается из потенциальной Wп и кинетической Wк энергии волны. При чем 

 

                                           Wк = mV ²/2.

 

       С другой стороны, полная энергия электрона в атоме водорода (без учета внутренней энергии главной волны, обеспечивающей динамическое равновесие с окружающим эфиром *) может быть определена исходя из следующих соображений.

       Максимальная энергия Wmax с учетом замечания *, которую мог бы иметь изначально спокойный электрон в атоме водорода, равна его максимальной потенциальной энергии, то есть потенциальной энергии спокойного электрона, находящегося на бесконечно удаленном расстоянии от протона:

rО  ke2                      ke2     ke2        Wmax = ò ¾¾¾ dR = 0 – (  - ¾¾ )= ¾¾ ,              ¥    R2                rО      rО

                        

 

 

 

 

 

 

 

где r_o – радиус электрона в фазе раскрытия (см. рис. 1 "б", если принять r₁ = r₀). На расстоянии r₁ потенциальная энергия электрона должна рассчитываться по формуле

 

                                     W_п1 = Wmax - ke² / r₁ 

 

Соответственно на расстоянии r₂:

 

                                       W_п2 = Wmax - ke² /r₂

 

      Кинетическая энергия, которую могут  иметь поперечные волны в главной волне  электрона на расстоянии r от центра электрона, определяется из равенства mV ² = ke²/r, то есть, поделив обе части равенства на 2, находим: mV²/2 = ke²/2r. Таким образом, полная энергия электрона на расстояниях r₁  и   r₂  должна рассчитываться по формулам:

6                    W₁ = W_max - ke² / r₁ + ke²/2r₁  = W_max - ke² / 2r₁

7                    W₂ = W_max - ke² /r₂  + ke²/2r₂  = W_max - ke² / 2r₂

 

       В общем случае энергия электрона в атоме водорода выражается формулой:

 

 8                                    W = W_max - ke² / 2r

 

         Эта формула является другим уравнением, которое должно было использоваться Бором в системе из двух уравнений при выводе формулы спектральных серий водорода. В этом случае с увеличением расстояния r  количество волн n увеличивается, а вместе с тем  растет  полная энергия электрона. При  этом, если  r₁  <   r₂, то W₂ – W₁ > 0, то есть как энергия электрона, так и излучаемая им энергия всегда положительны.

     Теперь, зная все это, можно сказать, что правильная формула спектральных серий атома водорода была получена Бором случайно, так как   

        W₂ – W₁  =  W_max - ke² / 2r₂   -  ( W_max - ke² / 2r₁ )   =   ke² / 2r₁ - ke² / 2r_2,

 

То есть по абсолютной величине разность энергий между энергетическими состояниями, принимаемая Бором, равна фактической.

     В соответствии с новой концепцией строения материи дискретность энергетических состояний электрона объясняется зависимостью его энергии от количества вторичных волн в нем, так как это количество  может иметь только целое значение. Вместе с переходом электрона из одного энергетического состояния в другое, происходит перераспределение энергии. При этом с уменьшением W , частично или  полностью, теряются   вторичные волны. Поглощение энергии всегда связано с увеличением количества вторичных волн в электроне.

    Возможные схемы атома водорода, при значениях  n от 1 до 3, приведены на рис. 1. Протон обозначен позицией 2, электрон 1 –   в фазе раскрытия.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

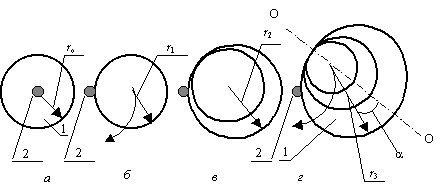
                                                            Рис. 1

 

 

      На схемах не показаны поперечные волны.

      В заключение, решив  систему  уравнений, сделаем   расчет скорости  V при   n = 1:

 

                     2pke²            2×3.14×9×10⁹(1.6×10^-19)²

             V = ¾¾¾ = ¾¾¾¾¾¾¾¾¾¾¾¾ = 2.186×10⁶ м/сек

                       h                        6.62×10^-34

 

     На эту  скорость  почему-то  никто  не  обратил  внимания. Вместе с  тем, она  весьма примечательна, являясь одной из констант. Исходя из новой теории строения материи, эта скорость равна скорости распространения вторичных волн в теле главной волны невозбужденного электрона в электрическом поле протона, то  есть  скорости распространения  волн  в эфире, находящемся в состоянии b-Г. Любопытно заметить, что

                            C/V = 2.998×10⁸/2.186×10⁶ = 137 ,

то есть известной в современной физике константе.

          Орбитальный момент импульса электрона, как это видно на рисунке, равен mVr, где V – мгновенная скорость электрона по касательной r₃ (см. рис. 1 "г").  Импульс вторичных волн не совпадает по направлению с общим орбитальным импульсом на угол a. Таким образом, орбитальный момент импульса Р может быть выражен через импульс вторичных волн, и он, очевидно, будет иметь дискретные значения:

                                                     Р = P_n×cos a,

где Р_n – момент импульса вторичных волн электрона.

        В современной физике эта величина принята равной:

 

 

 

 

 

 

 

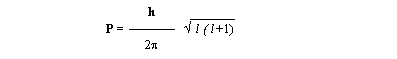
где l – орбитальное квантовое число, принимающее значения от 0 до n – 1.

     Вращаясь вокруг протона, электрон вызывает вращение сферонов. По этой причине возникают магнитные импульсы, которые зависят от скорости вращения, а вместе с тем от количества вторичных волн в главной волне электрона.